Kvadratne matrice
1. Teorija
Ako se radi o velikom broju promenljivih, praktično je da se one rasporede po vrstama i kolonama. Tada kažemo da te promenljive formiraju dvodimenzionalan niz, matricu, odnosno tabelu. Sve promenljive imaju zajedničko ime, a razlikuju se po mestu u vrsti i koloni. Npr. A[1,2] znači da je promenljiva sa imenom A u drugom redu i trećoj koloni.
Da se podsetimo iz prethodne lekcije: Osnove rada sa matricama
Već smo naučili da je matrica niz nizova, ili drugačije - dvodimenzionalni niz. Svakom elementu matrice pristupamo preko dva indeksa. Možete ih posmatrati kao indeks glavnog niza i indeks podniza, kao horizontalu i vertikalu, kao koordinate elementa - bilo koja definicija nam "završava posao".
Ako matrica ima isti broj redova i kolona, onda je to specifičan slučaj, tzv. kvadratna matrica.

Brojevi aij su elementi dvodimenzionalnog niza ili matrice, gdje je i indeks broja vrste, a j indeks broja kolone.
******************************************************
Ako je m<>n – pravougaona matrica ***
m=n – kvadratna matrica ***
*****************************************************
Dijagonale matrice
Kvadratna matrica nas zanima i zato što ima glavnu i sporednu dijagonalu. Glavna dijagonala ide od gornjeg-levog do donjeg-desnog elementa, a sporedna od gornjeg-desnog do donjeg-levog.
Glavna dijagonala
Elementi glavne dijagonale imaju iste indekse reda i kolone (i=j), Iznad
glavne dijagonale je indeks reda manji od indeksa kolone, a ispod glavne
dijagonale je indeks reda veći glavne dijagonale. Elementi a00,a11,
a22, ..., an-1,n-1
čine glavnu dijagonalu.
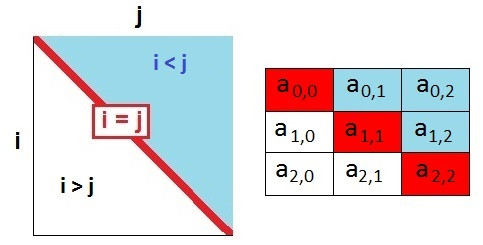
Slika 1. Glavna dijagonala i=j
Sporedna dijagonala
Elementi an-1,0,an-2,1 ..., a0,n-1 čine sporednu
dijagonalu.
Suma indeksa sporedne dijagonale je manja za 1 od dimenzije
kvadratne matrice-dvodimenzionalnog niza (i+j = n-1).
- Indeksi elemenata
matrice ispod sporedne dijagonale zadovoljavaju nejednačinu i+j > n-1,
a
- za elemente iznad sporedne dijagonale važi da zadovoljavaju nejednačinu i+j < n-1.
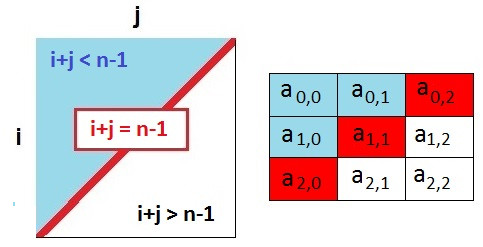
Slika 2. Sporedna dijagonala i+j = n-1
Dijagonalna matrica – svi elementi nula osim na glavnoj dijagonali
Transponovanje matrice
Transponovanje matrice predstavlja "obrtanje" matrice u smislu da redovi postaju kolone, a kolone redovi.
To znači da od matrice dimenzija NxM dobijamo matricu dimenzija MxN.
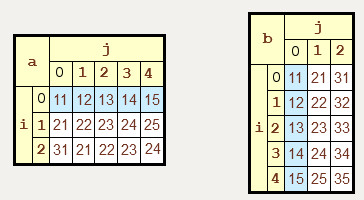
Plavom bojom smo obeležili prvi red matrice kako biste lakše ispratili šta se dešava sa elementima prilikom transponovanja.
Kako to izvesti: Najjednostavnije objašnjenje transponovanja je da se element sa pozicije [i,j] prebacuje na poziciju [j,i].